Monte Carlo Analyse
Was sie hier lesen, steht eigentlich in der Hilfe von LTspice (nur nicht so schön 😀), aber viele trauen sich da nicht dran, wohl wegen der vielen Klammern...
Ich möchte Ihnen hier mittels eines Beispiels die Angst davor nehmen.
Was macht eine Monte Carlo Analyse?
Nun, in einfachen Schaltungen können Sie Toleranzen von Bauteilen meist recht einfach berücksichtigen.
Mit steigender Komplexität ist das häufig nicht mehr so einfach machbar. Toleranzen beeinflussen Schaltschwellen, Verstärkungsfaktoren oder den Frequenzgang, oft eine Kombination von all diesen.
Eine Monte-Carlo-Analyse simuliert Ihre Schaltung viele Male und setzt jedes Mal die aktuellen Werte für jedes einzelne Bauteil auf einen zufälligen Wert innerhalb der angegebenen Toleranz. Diese Zufälligkeit, wie in einem Roulette-Spiel in dem berühmten Casino, gab der Methode ihren Namen.
Faites vos jeux!
Les jeux sont faits, rien ne va plus.
Sie bekommen also nicht nur eine Kurve für z.B. Vout, sondern eine Kurvenschar und können aus den Extremwerten die Auswirkungen der Toleranzen sehen.
Beispiel: Instrumentenverstärker
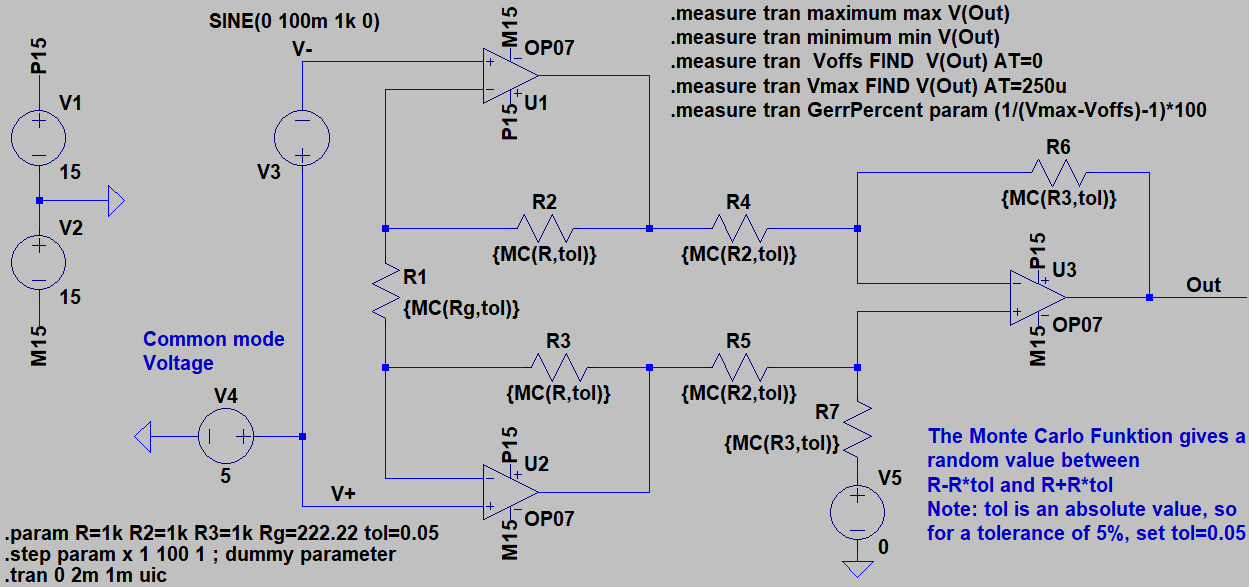 Ich habe für das Beispiel die Schaltung eines Instrumentenverstärkers gewählt.
Dieser reagiert sehr empfindlich auf Toleranzen von Bauteilen und
scheint mir deshalb prädestiniert für diese Demonstration.
Ich habe für das Beispiel die Schaltung eines Instrumentenverstärkers gewählt.
Dieser reagiert sehr empfindlich auf Toleranzen von Bauteilen und
scheint mir deshalb prädestiniert für diese Demonstration.
Laden Sie die Schaltung herunter und spielen Sie mit ihr.
V3 ist das Eingangssignal. Die Verstärkung ist durch R1 auf 10 eingestellt. Die 100 mV Eingangssignal sollten also 1 V am Ausgang ergeben. Mit V4 können Sie ein Common-Mode-Signal hinzufügen. Dieses verschlechtert insbesondere auch die Offset-Spannung.
Da in meinem Beispiel nur Widerstände das Verhalten bestimmen, habe ich auch nur einen Parameter tol, der die Toleranz der Widerstände beschreibt. In anderen Schaltungen mögen Sie vielleicht ein Rtol, ein Ctol und ein Ltol haben, vielleicht auch noch andere.
Wie setzt man nun die Monte-Carlo-Formel ein?
Normalerweise geben Sie bei einem Widerstand einfach den Wert von z.B. 10 k an.
Wollen wir nun eine Monte-Carlo-Analyse durchführen, setzen wir stattdessen die Monte-Carlo-Funktion ein: {MC(10k,0.05)}. LTspice setzt nun für jeden Durchlauf der Simulation einen zufälligen Wert zwischen 10 k-(10 k*0.05) und 10 k+(10 k*0.05) ein. Die geschweiften Klammern sagen LTspice, dass der Ausdruck kein fester Zahlenwert ist, sondern berechnet werden muss.
Natürlich können sowohl Wert als auch Toleranz auch ein Parameter sein, so wie wir es auch im Beispiel sehen, da wir hier viele Widerstände haben, die gleich groß sind, und auch die Toleranz kann man so sehr schnell für alle Widerstände anpassen.
Um die gewünschte Anzahl an Durchläufen zu erreichen, benötigen wir einen Dummy-Parameter: .step param x 1 100 1. Der Wert x, der hier von 1 bis 100 in Einerschritten durchläuft, wird nirgends benötigt, aber das Kommando sorgt für 100 Durchläufe mit jeweils neu gewählten Toleranz-Werten.
 Es sei angemerkt, das LTspice hier mit pseudo-zufälligen Werten arbeitet.
Die 100 Werte sind bei jedem Start der Simulation wieder gleich.
Das hat wohl etwas mit Reproduzierbarkeit zu tun, bewirkt aber auch,
das ohne diesem Dummy-Parameter jede Simulation wieder das gleiche Ergebnis
ergibt (und kein neues, zufälliges).
Es sei angemerkt, das LTspice hier mit pseudo-zufälligen Werten arbeitet.
Die 100 Werte sind bei jedem Start der Simulation wieder gleich.
Das hat wohl etwas mit Reproduzierbarkeit zu tun, bewirkt aber auch,
das ohne diesem Dummy-Parameter jede Simulation wieder das gleiche Ergebnis
ergibt (und kein neues, zufälliges).
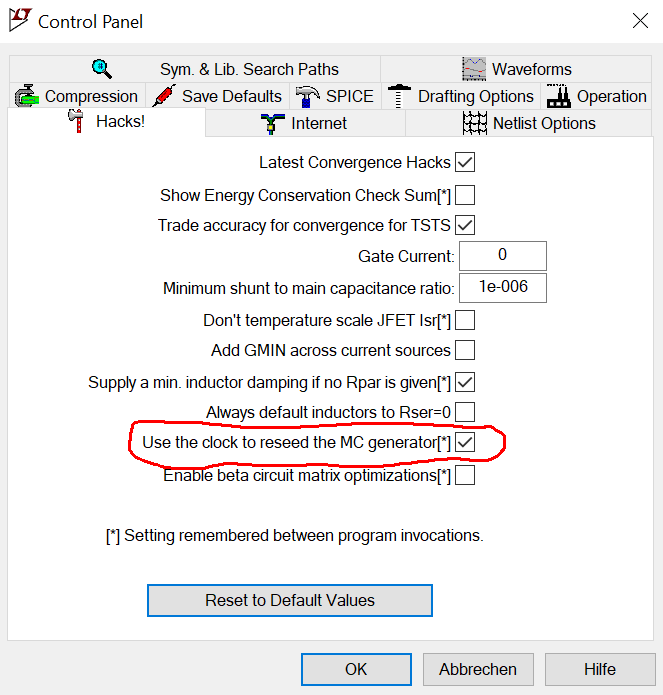
In den Einstellungen unter Hacks
können Sie einstellen, das die Uhrzeit
benutzt wird um den PRNG neu zu initialisieren. Dann bekommen Sie auch
für einzelne Simulationen unterschiedliche Ergebnisse.
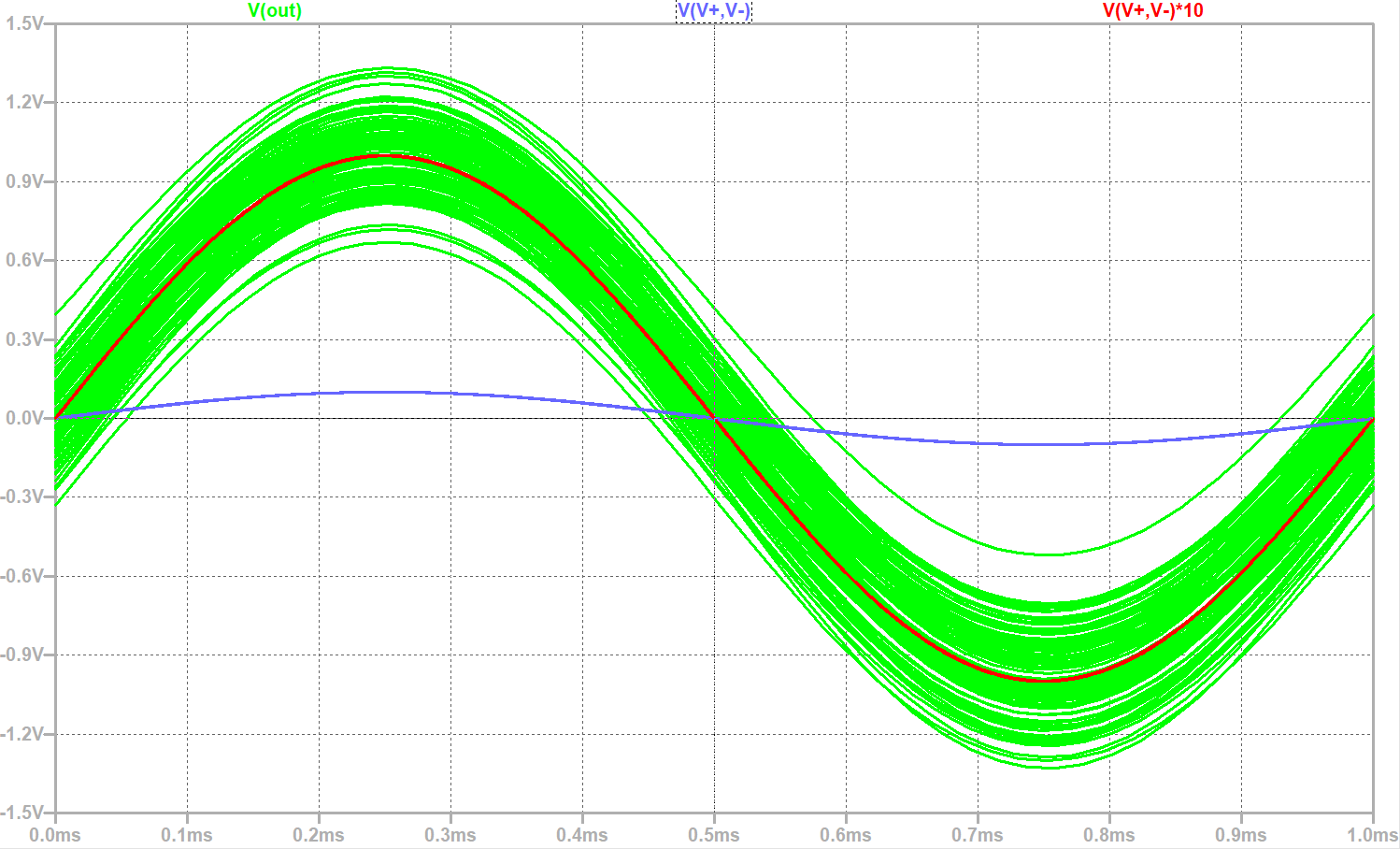 Hier sehen Sie das Ergebnis für die mit 5 % Toleranz bewusst schlecht dimensionierte
Schaltung, bei einer Common-Mode-Voltage (V4) von 5 V und 100 Durchläufen. Vout lässt zwar die Kurvenform erahnen, der absolute Wert schwankt jedoch
um mehr als 0,6 V, also fast ±40 %!
Selbst für einfache Messungen wäre
dies absolut unbrauchbar.
Hier sehen Sie das Ergebnis für die mit 5 % Toleranz bewusst schlecht dimensionierte
Schaltung, bei einer Common-Mode-Voltage (V4) von 5 V und 100 Durchläufen. Vout lässt zwar die Kurvenform erahnen, der absolute Wert schwankt jedoch
um mehr als 0,6 V, also fast ±40 %!
Selbst für einfache Messungen wäre
dies absolut unbrauchbar.
Zur Veranschaulichung habe ich das ideale Ausgangssignal in rot eingezeichnet.
Jetzt wissen Sie auch, warum man Instrumentenverstärker als fertig abgeglichenes Bauteil kauft, und nicht versucht, ihn selbst aufzubauen. Selbst mit 0,1 %-igen Widerständen kämen Sie kaum über 0,5 % Genauigkeit hinaus. Dabei sind die Fehlerbeiträge der OpAmps noch nichtmal berücksichtigt!
Und die Fehlergrenzen?
Dazu muss man ein bisschen tiefer eintauchen. Zumindest habe ich keine Methode gefunden, sie direkt zu ermitteln.
Ich habe einige .measure-Anweisungen in dieser Simulation platziert.
Interessant ist insbesondere die Anweisung:
.measure tran Voffs FIND V(Out) AT=0, die den
Offsetfehler ermittelt (bei t=0, wo wir auch 0 V Ausgangsspannung erwarten würden) und:
.measure tran GerrPercent param (1/(Vmax-Voffs)-1)*100,
die den Gain-Error in Prozent ermittelt.
Beide tun dies für jeden einzelnen Durchlauf und es ist mir nicht gelungen, direkt den maximalen Fehler daraus zu ermitteln.
 Im Spice-Error-Log (Strg+L oder View-Spice_
Im Spice-Error-Log (Strg+L oder View-Spice_
Drücken Sie dort die rechte Maustaste und wählen Sie Plot .step'ed .meas data
.
Dann öffnet sich ein neues Fenster und Sie können, wieder mit der rechten Maustaste,
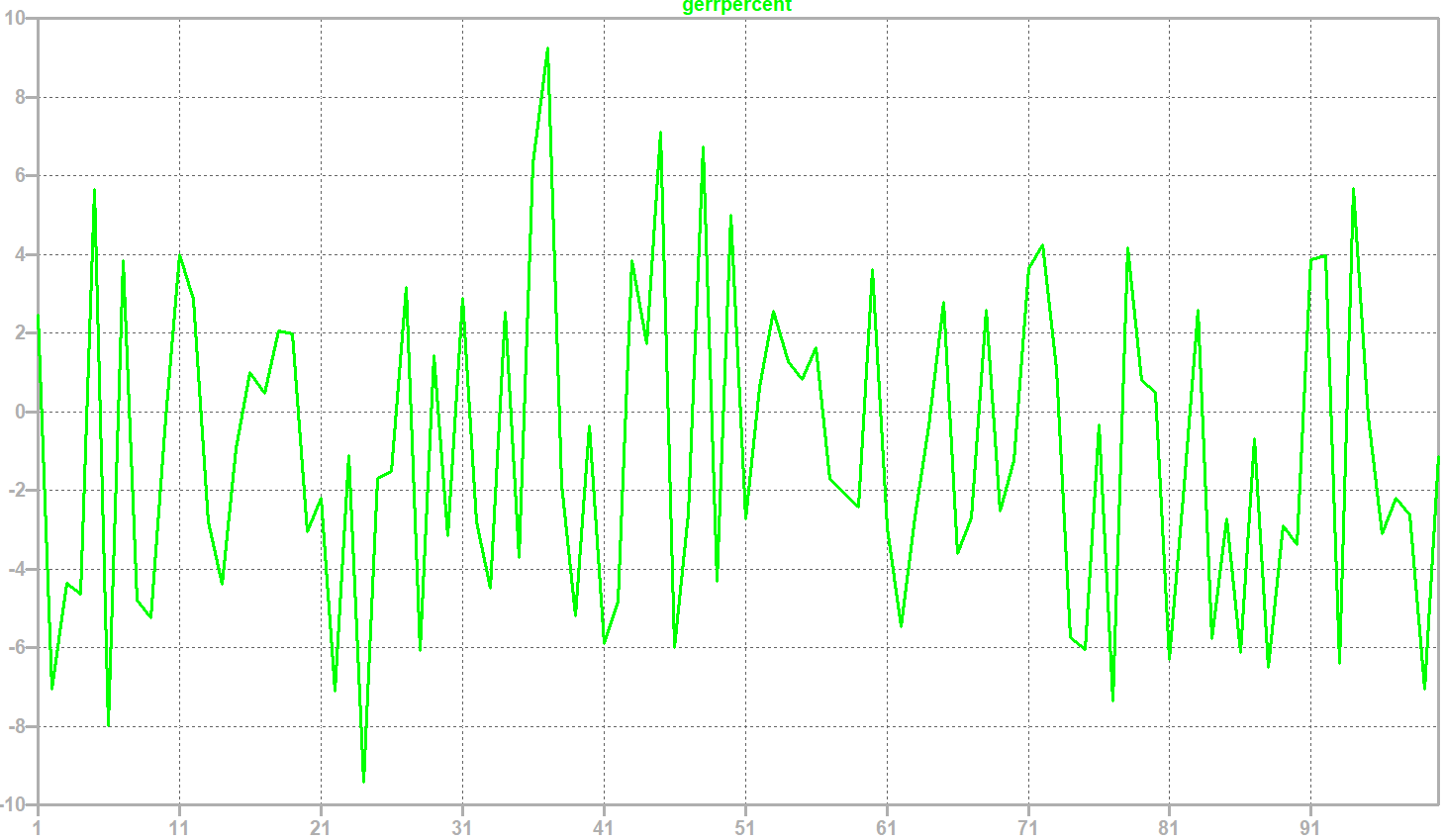
die gewünschten Kurven hinzu fügen. Im Diagramm sehen Sie beispielhaft den Gain-Error.
Man kann hier sehr schön sehen, das der maximale Fehler knapp ±10 % beträgt. Die geringe Zahl der extremen Ausschläge legt nahe, dass 100 Durchläufe zu knapp bemessen ist. Sie zeigt zwar die Richtung, aber wenn wir es genauer haben wollen, sollten wir besser 1000 Durchläufe wählen. Die Simulationszeiten steigen dabei natürlich entsprechend an. Für einen ersten Überblick reichen die 100 sicherlich, wenn wir wirklich die Grenzen sehen wollen, müssen wir deutlich mehr Durchläufe wählen, je mehr, desto besser. So viele, dass zumindest mehrere Extremwerte im ähnlichen Bereich liegen.

